R Tutorial Series: Two-Way Repeated Measures ANOVA

Repeated measures data require a different analysis procedure than our typical two-way ANOVA and subsequently follow a different R process. This tutorial will demonstrate how to conduct two-way repeated measures ANOVA in R using the Anova() function from the car package.
Note that the two-way repeated measures ANOVA process can be very complex to organize and execute in R. Although it has been distilled into just a few small steps in this guide, it is recommended that you fully and precisely complete the example before experimenting with your own data. As you will see, organization of the raw data is critical to successfully conducting a two-way repeated measures ANOVA using the demonstrated technique.

Tutorial Files

Before we begin, you may want to download the sample data (.csv) and sample idata frame (.csv) used in this tutorial. Be sure to right-click and save the files to your R working directory. This dataset contains a hypothetical sample of 30 participants whose interest in school and interest in work was measured at three different ages (10, 15, and 20). The interest values are represented on a scale that ranges from 1 to 5 and indicate how interested each participant was in a given topic at each given age.

Data Setup

Notice that our data are arranged differently for a repeated measures ANOVA. In a typical two-way ANOVA, we would place all of the values of our independent variable in a single column and identify their respective levels with a second column, as demonstrated in this sample two-way dataset. In a two-way repeated measures ANOVA, we instead combine each independent variable with its time interval, thus yielding columns for each pairing. Hence, rather than having one vertical column for school interest and one for work interest, with a second column for age, we have six separate columns for interest, three for school interest and three for work interest at each age level. The following graphic is intended to help demonstrate this organization method.

Treat time as if it were an independent variable. Then combine each independent variable with each level of time and arrange the columns horizontally.

Beginning Steps

To begin, we need to read our dataset into R and store its contents in a variable.

1. > #read the dataset into an R variable using the read.csv(file) function
2. > dataTwoWayRepeatedMeasures <- read.csv("dataset_ANOVA_TwoWayRepeatedMeasures.csv")
3. > #display the data
4. > #notice the atypical column arrangement for repeated measures data
5. > dataTwoWayRepeatedMeasures

The first ten rows of our dataset

idata Frame

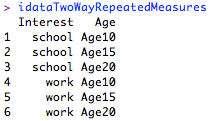
Another item that we need to import for this analysis is our idata frame. This object will be used in our Anova() function to define the structure of our analysis.

1. > #read the idata frame into an R variable
2. > idataTwoWayRepeatedMeasures <- read.csv("idata_ANOVA_TwoWayRepeatedMeasures.csv")
3. > #display the idata frame
4. > #notice the text values and correspondence between our idata rows and the columns in our dataset
5. > idataTwoWayRepeatedMeasures

The idata frame

Note that it is critical that your idata frame take the demonstrated form for this technique to work. I experimented with several alternative, perhaps more intuitive, layouts without success. It is particularly important to notice that both columns of the idata frame contain text values (not numerical ones - hence the repeated prefixing of Age to the values in every row of the Age column). Additionally, if you read the rows of the idata frame horizontally, you will see that they correspond precisely to the columns of our dataset. The following graphic is intended to help demonstrate this organization method.

Use only text values in your idata frame. Ensure that the rows of your idata frame correspond to the columns in your dataset.

Linear Model

Prior to executing our analysis, we must follow two steps to formulate our linear model to be used in the Anova() function.

Step 1: Bind the Columns

1. > #use cbind() to bind the columns of the original dataset
2. > interestBind <- cbind(dataTwoWayRepeatedMeasures$schoolAge10, dataTwoWayRepeatedMeasures$schoolAge15, dataTwoWayRepeatedMeasures$schoolAge20, dataTwoWayRepeatedMeasures$workAge10, dataTwoWayRepeatedMeasures$workAge15, dataTwoWayRepeatedMeasures$workAge20)

Step 2: Define the Model

1. > #use lm() to generate a linear model using the bound columns from step 1
2. > interestModel <- lm(interestBind ~ 1)

Anova(mod, idata, idesign) Function

Typically, researchers will choose one of several techniques for analyzing repeated measures data, such as an epsilon-correction method, like Huynh-Feldt or Greenhouse-Geisser, or a multivariate method, like Wilks' Lambda or Hotelling's Trace. Conveniently, having already prepared our data, we can employ a single Anova(mod, idata, idesign) function from the car package to yield all of the relevant repeated measures results. This allows us simplicity in that only a single function is required, regardless of the technique that we wish to employ. Thus, witnessing our outcomes becomes as simple as locating the desired method in the cleanly printed results.
Our Anova(mod, idata, idesign) function will be composed of three arguments. First, mod will contain our linear model. Second, idata will contain our data frame. Third, idesign will contain a multiplication of the row headings from our idata frame (in other words, our independent variables), preceded by a tilde (~). Thus, our final function takes on the following form.

1. > #load the car package (install first, if necessary)
2. library(car)
3. > #compose the Anova(mod, idata, idesign) function
4. > analysis <- Anova(interestModel, idata = idataTwoWayRepeatedMeasures, idesign = ~Interest * Age)

Results Summary

Finally, we can use the summary(object) function to visualize the results of our repeated measures ANOVA.

1. > #use summary(object) to visualize the results of the repeated measures ANOVA
2. > summary(analysis)

Relevant segment of repeated measures ANOVA results

Supposing that we are interested in the Wilks' Lambda method, we can see that there is a statistically significant interaction effect between interest in school and interest in work across the age groups (p < .001). This suggests that we should further examine our data at the level of simple main effects. For more information investigating on simple main effects, see the Two-Way ANOVA with Interactions and Simple Main Effects tutorial. Of course, in this case of repeated measures ANOVA, another way to break the data down would be to run two one-way repeated measures ANOVAs, one for each of the independent variables. In either instance, pairwise comparisons can be conducted to determine the significance of the differences between the levels of any significant effects.

Complete Two-Way Repeated Measures ANOVA Example

To see a complete example of how two-way repeated measures ANOVA can be conducted in R, please download the two-way repeated measures ANOVA example (.txt) file.

References

Moore, Colleen. (n.d.). 610 R9 -- Two-way Repeated-measures Anova. Retrieved January 21, 2011 from http://psych.wisc.edu/moore/Rpdf/610-R9_Within2way.pdf